Trigonometría
| Sitio: | Educación a Distancia - UNaM |
| Curse: | Matemática |
| Libro: | Trigonometría |
| Impreso por: | Cuenta visitante |
| Fecha: | sábado, 14 de febrero de 2026, 21:33 |
Descripción
VES 2022
Trigonometría
¿Recuerdan cómo se resuelven los problemas en los que deben relacionar y hacer cálculos con las medidas de los lados y los ángulos de un triángulo?
Como les dijimos en otras oportunidades, siempre debemos recuperar los conocimientos que tenemos de un tema - conocimientos previos -para poder vincularlos con los nuevos conocimientos. En este caso, revisar los conocimientos que tienen de trigonometría les va a permitir valorar lo que aprendieron con sentido, por eso recuerdan, o lo que indudablemente no lograron aprender con sentido, por eso no lo recuerdan. Esto justifica por qué primero les planteamos que resuelvan una actividad de autoevaluación.
No se olviden que para resolver cualquiera de las actividades que proponemos no deben recurrir primero a la guía de estudio. Precisamente lo que pretendemos es que revisen y valoren los conocimientos que tienen del tema. Luego, les invitamos a qué interactúen con las guía de estudio para aclarar dificultades o afianzar conocimientos del tema.
Ahora sí les presentamos esta actividad de autoevaluación.
De esta manera van a poner a prueba los conocimientos ya aprendidos de trigonometría.
¡Entremos en acción!

CLICK AQUÍ PARA CONTESTAR EL CUESTIONARIO DE AUTOEVALUACIÓN
UN POCO DE HISTORIA
La trigonometría surgió hace más de 2000 años cuando los griegos necesitaron resolver problemas prácticos relacionados con la astronomía. La astronomía de los matemáticos antiguos, como Pitágoras y sus primeros seguidores, en los siglos VI, V y IV a. de C., consistió fundamentalmente en descripciones y especulaciones aventuradas sobre los astros.
Más adelante se fue poniendo de manifiesto que era necesario hacer de la astronomía una ciencia más exacta, fundada en mediciones y en una matemática apropiada, que permitiera predecir con precisión, los eclipses y los movimientos de los astros, para hacer los calendarios más exactos y la navegación más segura. Así nació la trigonometría con Hiparco, un griego del siglo II a. de C.
Los tres matemáticos griegos a quienes más debe la astronomía antigua fueron Hiparco, del siglo II a. de C. y, sobre todo, Tolomeo, del siglo II d. de C., con quien la astronomía alcanza una de sus cumbres.
Una gran parte de los teoremas de nuestra actual trigonometría eran perfectamente conocidos y utilizados con destreza por Tolomeo.
Fuente: De Guzmán, M., Cólera, J. y Salvador, A.. Matemáticas, Bachillerato 2 (1987, p.44)
¿Qué significa resolver problemas de trigonometría?Resolver problemas de trigonometría significa hacer matemática relacionando y haciendo cálculos con las medidas de los lados y los ángulos de un triángulo. |
A continuación vamos a desarrollar el tema considerando cuatro apartados que incluyen conceptos claves para resolver distintas situaciones de trigonometría : ángulos y sistemas de medición de ángulos, triángulos y razones trigonométricas, resolución de triángulos rectángulos y resolución de triángulos oblicuángulos.
Durante este desarrollo se encontrarán con una serie de tutoriales. Los invitamos a que miren cada uno de ellos porque les ayudará a aprender con sentido a los conceptos de trigonometría.
ÁNGULOS Y SISTEMAS DE MEDICIÓN DE ÁNGULOS.
Un concepto clave en trigonometría es el de ángulo. Se les puede venir a la mente estas preguntas: ¿qué es un ángulo? , ¿cómo se mide un ángulo? , ¿cuáles son los sistemas de medición de ángulos? ¿cómo se realiza el pasaje de una medida de un ángulo en el sistema sexagesimal al sistema radial o viceversa?. Las respuestas encontrarán en estos dos tutoriales que preparamos para ayudarlos a comprender estos conceptos.

Video tutorial: Clasificación de Ángulos - Sistema sexagesimal de medición
Aunque es habitual medir ángulos en grados sexagesimales, para estudiar funciones trigonométricas, o en algunos casos resolver problemas, es conveniente utilizar el sistema circular o también conocido como sistema radial. Es decir, existe una relación que establece las equivalencias entre medidas de ángulos expresados en el sistema sexagesimal o radial . De esta manera, en la práctica pueden pasar la medida de un ángulo expresado en un sistema al otro.

Video tutorial: Sistema Circular de medición de ángulos - Equivalencia con el sistema sexagesimal
La búsqueda rápida de significados matemáticos
Deben tener en cuenta que entre los materiales de apoyo se encuentra un Breve Glosario Matemático. Es una herramienta de ayuda al estudio que les permite encontrar de manera rápida los significados de los conceptos matemáticos que no recuerdan o desconocen.

TRIÁNGULOS Y RAZONES TRIGONOMÉTRICAS
Nuestro conocimiento de los triángulos nos permite determinar los valores de las funciones trigonométricas de ciertos ángulos. Comencemos por recordar un teorema que es uno de teoremas más más conocidos en geometría: El teorema de Pitágoras.
→ Un teorema para recordar: Teorema de Pitágoras
Como hemos visto en el bloque 1 el teorema de Pitágoras es de gran utilidad para calcular las medidas de los lados de un triángulo rectángulo. Este tutorial les ayudará a recordar. ¡No se olviden que para utilizar este teorema el triángulo debe ser un triángulo rectángulo!

Video Tutorial: Teorema de Pitágoras
→Un concepto para recordar: alturas de un triángulo
Uno de los elementos más importantes de un triángulo es su altura. Más propiamente, deberíamos decir "sus alturas", en plural, puesto que un triángulo tiene tres alturas. Recuerden que la altura es la menor distancia entre un vértice y el lado opuesto (o su prolongación), por lo que a cada vértice le corresponde una altura.

El concepto de altura se aplica en muchas situaciones de resolución de triángulos en trigonometría. Por este motivo les proponemos que realicen esta actividad con el GeoGebra. Las consignas están en el mismo boceto del Geo.
https://www.geogebra.org/m/c7bzbd4c
→Más sobre triángulos rectángulos
En el Ejemplo 1 de la imagen se dan los datos de la medida de los dos catetos del triángulo y se pide la medida de la hipotenusa. Esta situación se resuelve utilizando el teorema de Pitágoras. Consideramos sólo la raíz positiva (raíz aritmética) porque no tiene sentido una medida de hipotenusa negativa.
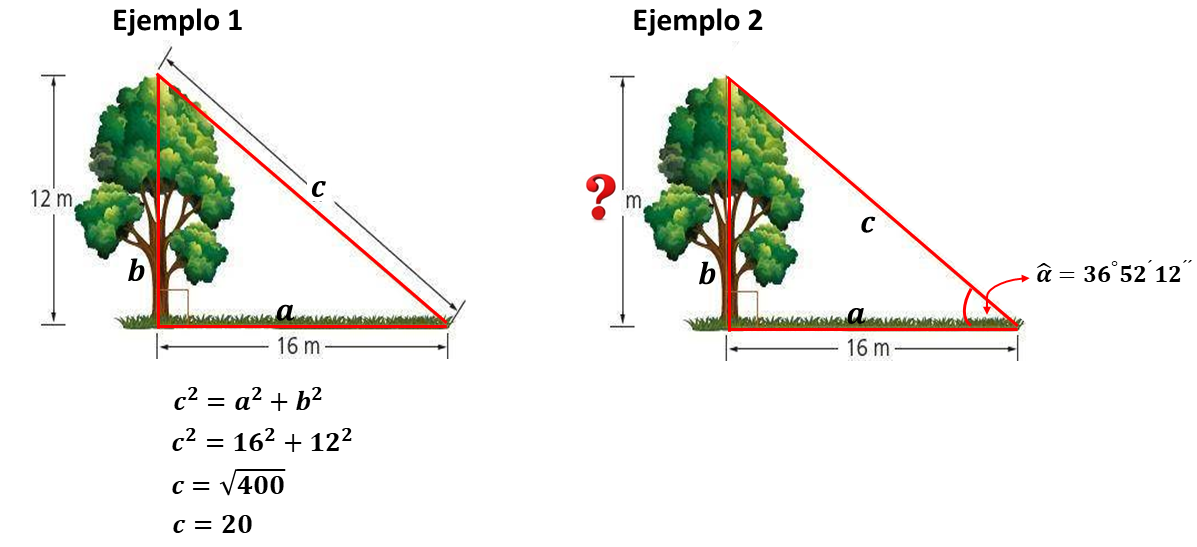
En el Ejemplo 2 se da un cateto y un ángulo y se pide la medida del otro cateto que representa la altura del árbol. Para resolver este tipo de situaciones habría que relacionar dos lados con un ángulo. Este tipo de relaciones se llaman razones trigonométricas de los ángulos. Este tutorial explica de manera sencilla las razones trigonométricas.

Video tutorial: Razones Trigonométricas en un triángulo rectángulo
|
Intenten los siguiente Resuelvan el ejercicio del Ejemplo 2 utilizando los conceptos desarrollados en el tutorial de razones trigonométricas.¿Podrían anticipar el resultado antes de resolver? |
En el Ejemplo 3 se dan los datos de las medidas de un cateto y la hipotenusa y se pide la medida del ángulo α .
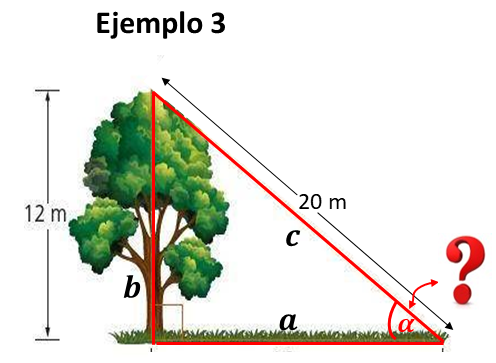
Para resolver situaciones de este tipo se utilizan las funciones trigonométricas inversas. Se viene el tutorial con un ejemplo de aplicación.

Video Tutorial: Funciones trigonométricas inversas
|
Intenten lo siguiente Resuelvan el ejercicio del Ejemplo 3 utilizando los conceptos desarrollados en este último tutorial. ¿Podrían anticipar el resultado antes de resolver? |

Escriban un argumento convincente explicando por qué se cumplen estas dos relaciones fundamentales:
- RESOLUCIÓN DE TRIÁNGULOS RECTÁNGULOS
El conocimiento de los conceptos desarrollados anteriormente les permitirá ya resolver triángulos rectángulos. Resolver un triángulo consiste en averiguar, mediante razonamientos, fórmulas o construcciones, los elementos desconocidos. Por ejemplo, determinar las medidas de algunos lados y ángulos de un triángulo rectángulo.
A continuación les proponemos que miren estos dos tutoriales en el primero se explica que significa resolver un triángulo y las fórmulas empleadas para ello y se muestra la resolución de un triángulo rectángulo si los datos son los catetos y en el segundo se muestra la resolución de un triángulo rectángulo si los datos son: a) un cateto y la hipotenusa; b) la hipotenusa y un ángulo; c) un ángulo y un cateto.
♦ Parte 1: los datos son los dos catetos

Video tutorial: Resolución de triángulos rectángulos (Parte 1)
♦Parte 2: los datos: a) un cateto y la hipotenusa; b) son un lado y un ángulo.

Video tutorial: Resolución de triángulos rectángulos (Parte 2)
- RESOLUCIÓN DE TRIÁNGULOS OBLICUÁNGULOS
Ya conocen cómo pueden aplicarse las definiciones de seno, coseno y tangente de un ángulo en la resolución de triángulos rectángulos. Sin embargo, tanto en la teoría como en las aplicaciones, pueden presentarse problemas en los que sea necesario obtener las medidas de ángulos y lados de triángulos no rectángulos.
En forma análoga a lo que vimos con triángulos rectángulos, son diversas las situaciones en la que surge la necesidad de resolver un triángulo oblicuángulo. Les presentamos una de ellas:

Para resolver estos casos son útiles dos teoremas, conocidos como "teorema del seno" y "teorema del coseno". Vean el siguiente tutorial que utiliza estos teoremas en la resolución de triángulos oblicuángulos.

Video Tutorial: Resolución de triángulos oblicuángulos- Teoremas del Seno y Coseno

Esta Guía de actividades tiene el propósito que puedan profundizar el estudio de los conceptos trabajados de trigonometría. Pueden utilizar la FICHA DE ESTUDIO que les ayudará a tener a mano algunas relaciones y propiedades que se aplican en la resolución de triángulos de distinto tipo.
FICHA DE ESTUDIO

CLICK AQUÍ PARA RESOLVER LA GUÍA DE ACTIVIDADES DE TRIGONOMETRÍA
¿Qué dificultades matemáticas han tenido? ¿Qué estrategias utilizaron para superar las dificultades?

CUESTIONARIO DE EVALUACIÓN FINAL DEL BLOQUE 5
Ahora llegó el momento de la autoevaluación final del Bloque 5. No olviden que esta actividad forma parte de este proceso de aprendizaje que están transitando. Tengan en cuenta que es tan importante aprender con sentido los conceptos matemáticos como aprender a valorar, criticar y a reflexionar sobre el proceso de aprendizaje individual realizado.


CLICK AQUÍ PARA CONTESTAR EL CUESTIONARIO

