Números, Ecuaciones lineales y Sistemas de ecuaciones lineales
| Sitio: | Educación a Distancia - UNaM |
| Curse: | Matemática |
| Libro: | Números, Ecuaciones lineales y Sistemas de ecuaciones lineales |
| Impreso por: | Cuenta visitante |
| Fecha: | martes, 23 de septiembre de 2025, 12:18 |
Descripción
Libro
EL LENGUAJE DE LA MATEMÁTICA
Para poder aprender Matemática es fundamental comprender el lenguaje que utiliza esta hermosa ciencia. Si no comprenden el lenguaje, el aprendizaje de los conceptos matemáticos será mecánico y memorístico. En ese caso no estarían transitando el camino del buen aprendizaje matemático.
También es necesario reflexionar sobre la pregunta: ¿Qué es aprender Matemática?. Deben tener en cuenta que los significados que otorgan a esta pregunta son los que orientan sus acciones cuando aprenden. Aquí les proponemos aprender Matemática promoviendo estrategias que les permitan "aprender construyendo el sentido de los conocimientos matemáticos" . Entendemos que así estarían orientados hacia un buen aprendizaje matemático.
En el video que aparece a continuación les presentamos algunas ideas relacionadas a estas cuestiones.
.

Video tutorial: El lenguaje de la Matemática

¿Qué diferencias o similitudes encuentran entre la idea actual que tienen de qué es aprender Matemática y la que se expresa en el video? Escriban su respuesta en un cuaderno de anotaciones porque la retomaremos más adelante.
NÚMEROS
¿Qué diferencias o similitudes encuentran entre la idea actual que tienen de qué es aprender Matemática y la que se expresa en el video? Escriban su respuesta en un cuaderno de anotaciones porque la retomaremos más adelante.
La noción de número es tan antigua como el hombre mismo. Las tribus más primitivas -tanto en tiempos pasados como en la actualidad- disponían de símbolos para contar; pero hasta la Edad de Bronce no aparecieron sistemas de numeración para manejar números grandes y realizar operaciones entre ellos.
Los sistemas de numeración se fueron enriqueciendo progresivamente y están profundamente unidos al progreso matemático y cultural de los pueblos. La tabla siguiente es una muestra de esta afirmación.
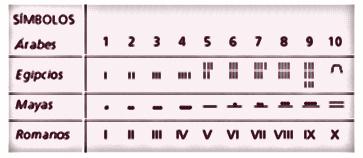
Hay numerosas situaciones reales que, para ser resueltas, requieren del uso de los números. Por eso, en la actualidad, continúa siendo muy importante conocer sus características, sus propiedades y las operaciones con números. Entonces empecemos con una actividad que les lleve a PENSAR CRÍTICAMENTE sobre los números.
Un conjunto numérico es cerrado bajo una operación si, siempre que la operación se realice con elementos del conjunto, el resultado también es un elemento del conjunto.
Determinen si los siguientes conjuntos de números son cerrados bajo la operación indicada (Ayúdense con ejemplos).
a) El conjunto de números naturales (N) y la operación sustracción.
b) El conjunto de enteros (Z) y la operación división.
Con la realización de esta actividad pudieron reconocer que en Naturales no siempre es posible la sustracción y que en Enteros no siempre es posible la división. Estos son sólo dos ejemplos de cómo la necesidad de hacer posible la resolución de operaciones impuso la creación de distintos tipos de números. La Clasificación de números les permitirá recordar por qué se justifica la creación de cada uno de ellos.
• CLASIFICACIÓN DE NÚMEROS Y OTRAS CARACTERÍSTICAS •
Seguramente habrán estudiado en la escuela secundaria esta representación de clasificación de los números:
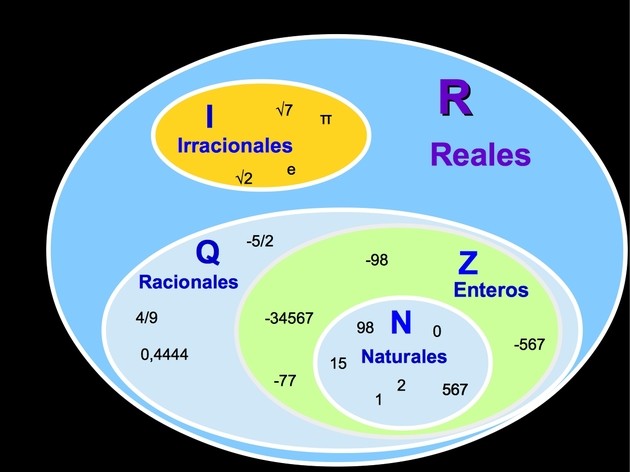
¿Recuerdan esta clasificación? Miren este video tutorial que preparamos sobre Clasificación de números a partir de una actividad. Podrán observar las relaciones de inclusión entre los distintos conjuntos numéricos. Siempre viene bien recuperar los conocimientos ya aprendidos.
.

Video tutorial: Clasificación de Números
Destacamos algunas de las características de los distintos conjuntos numéricos que se exponen en el video tutorial:
- El conjunto de los números naturales (N) es infinito pero es el único conjunto numérico que tiene un primer elemento.
- El conjunto de números enteros (Z) es el único conjunto en el que cada elemento tiene un antecesor y sucesor.
- Las fracciones y las expresiones decimales finitas o infinitas periódicas representan números racionales (Q).
- Todas las fracciones equivalentes entre sí representan el mismo número racional. Ejemplo:
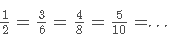
- Un número irracional (I) es una expresión decimal infinita y no periódica. Por eso un número irracional no se puede expresar como una fracción
- El conjunto de los números reales (R) es la unión del conjunto Q y el conjunto I . Por tanto el conjunto R incluye a todos los conjuntos numéricos.
¿Qué es la sucesión de Fibonacci? ¿por qué es tan importante esta sucesión ?
Ahora les proponemos esta actividad de clasificación de números, en la que pondrán en juego los conocimientos que ya tienen, conocidos como conocimientos previos, y, acaso, también, sus estrategias de ingenio. En diferentes momentos del bloque les propondremos actividades que tienen esta intención.
RECUERDEN que para resolver cualquiera de las actividades de autoevaluación que proponemos no deberían recurrir primero a la Guía de Estudio. Precisamente lo que pretendemos es que revisen y valoren los conocimientos que tienen del tema. Luego, les invitamos a que interactúen con la Guía de Estudio para aclarar dificultades o afianzar conocimientos del tema.
.

CLICK AQUÍ PARA RESPONDER EL CUESTIONARIO DE CLASIFICACIÓN DE NÚMEROS
Si los resultados que obtuvieron no son óptimos, ¡NO SE DESANIMEN!

Luego de responder esta pregunta, miren nuevamente el video tutorial, acudan a la Guía de Estudio para que los oriente en relación al tema y revisen nuevamente los errores que cometieron en la resolución de la actividad. Les animamos a que creen el hábito de reflexionar sobre los errores. Como desafío personal, realicen por segunda vez la Actividad de Clasificación de Números.
.

.
• LA NECESIDAD DE RECONOCER LAS DISTINTAS FORMAS DE REPRESENTACIÓN DE LOS NÚMEROS •
En el video tutorial de clasificación de números han visto que existen diferentes formas de expresar un número. Ejemplos: 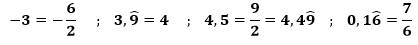
Esto significa que es necesario reconocer los conjuntos numéricos y las distintas formas de representación de un número. También es muy útil para la interpretación en la recta numérica, la realización de cálculos (porcentajes, proporciones, áreas y volúmenes), aproximaciones, la resolución de ejercicios combinados, etc.
Respecto a este tema, podemos decir que es habitual que confundan las distintas formas de representación de los números racionales, como el caso de los decimales periódicos y las fracciones. Y este concepto además es clave para poder representar decimales periódicos en la recta numérica. Por este motivo elegimos este tutorial que les ayudará a recordar.
.
 .
.
Video Tutorial: Conversión de una expresión decimal periódica a fracción
→Para tener en cuenta con las expresiones decimales periódicas: En general es posible probar que si se tiene una expresión decimal periódica con período 9, y dicha expresión es:
-
Periódica pura, representa un número entero. Por ejemplo:
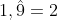 y
y 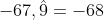
-
Periódica mixta, hay una expresión equivalente finita. Por ejemplo:
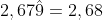 y
y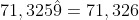
Es importante tener en cuenta que los números racionales que tienen una expresión decimal finita tienen, en realidad, dos expresiones decimales distintas: la expresión finita, y otra infinita periódica, con período 9. La expresión infinita se obtiene disminuyendo en 1 el último dígito de la representación finita, y agregando a continuación el dígito 9 en forma periódica.
Por ejemplo: 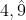 y 5 son las expresiones decimales del número racional 5;
y 5 son las expresiones decimales del número racional 5; 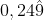 y 0,25 son las expresiones decimales del número racional
y 0,25 son las expresiones decimales del número racional 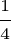
En cambio, los números racionales con expresión decimal periódica distinta de 9 tienen una sola expresión decimal.
Los números en la recta numérica
Esos números que se clasificaron en el tutorial Clasificación de números también se pueden ordenar, por esta razón se pueden representar gráficamente en una recta. Los números se representan como puntos sobre una recta continua en la que fijamos un origen y una unidad.
.

.
Video tutorial: La recta numérica
Considerando la representación de los números reales presentada en el video, es oportuno señalar:
- A cada punto de la recta se le puede hacer corresponder un único número real, es decir se puede definir una correspondencia uno a uno entre puntos de la recta y números reales (Axioma de Completitud). Por eso se habla de recta numérica y de que el conjunto de números reales es el único que completa la recta.
- Entre dos números racionales siempre hay infinitos racionales. Por este motivo decimos que el conjunto de números racionales es denso.
- Entre dos números irracionales cualesquiera hay infinitos números irracionales; esto significa que también el conjunto de números irracionales es denso.
El conjunto de los números reales es denso
- El conjunto de números reales es totalmente ordenado por la relación menor o igual
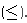
¿Qué sucede cuando elevan 0 a la potencia cero?
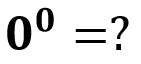
La búsqueda rápida de significados matemáticos
Entre los materiales de apoyo se encuentra un Breve Glosario Matemático. Es una herramienta de ayuda al estudio que les permite encontrar de manera rápida los significados de los conceptos matemáticos que no recuerdan o desconocen. ¡Ténganlo en cuenta!
.

.
LOS NÚMEROS EN ACCIÓN
Están familiarizados nuevamente con los números según el conjunto numérico al que pertenecen y sus diferentes formas de representación. Ahora es importante que reconozcan y utilicen los números y operaciones, comprendiendo las propiedades que los definen y sus diferentes formas de representación en función de la situación problemática a resolver.
Para avanzar en ese sentido les proponemos que resuelvan tres situaciones concretas en las que se ponen en juego los números Enteros, los Racionales y los Reales (en ese orden). Las situaciones son concretas porque la intención en este módulo es, en lo posible, unificar la Matemática que aprendieron en la escuela con la que se utiliza fuera de ella, es decir, aquella que las personas utilizan en la vida cotidiana.
A continuación de la resolución de cada situación concreta, les planteamos que resuelvan una Guía de actividades con las soluciones incluidas para que practiquen las operaciones con números y sus propiedades. Aprender matemática es casi sinónimo de resolver situaciones problemáticas de distinto tipo. Por ello, en las guías de actividades de números, además de ejercicios se incluyen problemas en los que se incorporan otros conceptos, como figuras geométricas, fórmulas de área, concepto de medida, entre otros.

→Los Números Enteros (Z): Números para contar
Se dice que el mes de junio tiene 30 días. Análogamente se cuentan los integrantes de una de una familia o los años que transcurrieron desde el nacimiento de una persona. En fin, contamos con los primeros números que aprendimos en la escuela: los números naturales. Podemos decir entonces que los números naturales que ya conoces 0,1, 2, 3, .....8,9,10,......sirven para contar.
Los números naturales también sirven para ordenar (numerar). Por ejemplo, la clase de Matemática es a la 5° hora o es una materia que se dicta en 1° año de la Facultad.
A veces, para contar, se requieren cantidades negativas. Por ejemplo, en Historia, el año -320 es el año 320 años antes de Cristo o las temperaturas.
Realicen la próxima actividad en la que aparecen los números enteros en acción.
El Almacén de Doña María
Doña María, dueña de un almacén, es muy confiada. En la pared de su negocio hay un cartel que dice “HOY SE FÍA”.
Si van a comprar al almacén de doña María, les puede ocurrir que su gasto sea menor, igual o superior al dinero que llevas. En el último caso, les quedan debiendo. Vean el cuaderno de anotaciones de doña María en el que aparece una tabla con los datos referidos al dinero que gastó cada cliente y al dinero que llevó para hacer las compras.
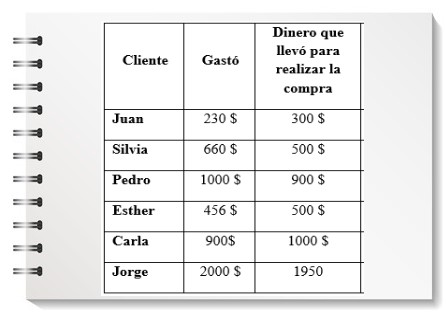
Resuelvan esta actividad para ayudar con las cuentas a Doña María

CLICK AQUÍ PARA RESPONDER EL CUESTIONARIO El Almacén de Doña María

¿Cómo les fue con la ayuda a Doña María? ¿Qué dificultades matemáticas han tenido? ¿Qué estrategias utilizaron para superar las dificultades?
Operaciones combinadas con Números Enteros
En las operaciones con números enteros, una de las dificultades que se les plantea es cómo interpretar los signos de los números vinculados con las operaciones y el orden en el que se resuelven las operaciones. Por este motivo elegimos este video tutorial para que puedan comprender mejor este procedimiento.

Video tutorial: Operaciones combinadas con Números Enteros
Es conveniente...
- Primero separar en términos. Los signos + y - separan en términos.
- Evaluar si es conveniente suprimir paréntesis, corchetes o llaves, considerado la operación que precede al paréntesis, corchetes o llaves o resolver primero las operaciones que están dentro de ellos.
- Resolver potencias y raíces, multiplicaciones y divisiones, sumas y restas, en ese orden.
Para resolver los ejercicios combinados es muy importante, además, recordar la definición de las operaciones con números y las propiedades que cumplen. Así podrán aplicarlas correctamente en la resolución.
Las FICHAS DE ESTUDIO son materiales de apoyo al estudio que sirven para recordar conceptos, por ejemplo, en este caso, las operaciones y propiedades. A continuación les presentamos dos fichas de estudio como ejemplos.
- Ficha de estudio de la operación potenciación y sus propiedades.
Lean comprensivamente y analicen la información que se presenta en la ficha de estudio. No hay una única manera de elaborar una ficha de estudio porque no se olviden que en el aprendizaje cada uno pone en juego su propia representación mental del contenido, selecciona la información que considera relevante e interpreta en función a sus conocimientos previos. Y este proceso de construcción es individual. Va otro ejemplo.
- Ficha de estudio de la operación radicación y sus propiedades.
Si lo creen necesario, pueden construir otras fichas de estudio sobre otros conceptos que consideran que todavía necesitan recordar y fijar, que todavía no pudieron aprender. Una vez que lograron un buen aprendizaje del contenido , seguramente irán abandonando gradualmente el uso de la ficha.

- El recíproco de un número racional distinto de cero, ¿es racional o es irracional?
- ¿Cuál es el recíproco del 40%?
Tomando la idea del gran matemático Paul Hamos, van a hacer Matemática resolviendo una Guía de actividades de Números Enteros.

En esta Guía de actividades de Números Enteros encontrarán situaciones de distinto tipo sobre el tema. Si necesitan orientación sobre el estudio de los números enteros tienen la Guía de estudio que les ayudará en este sentido. En ella también encontrarán más actividades para resolver por si quieren intensificar su aprendizaje matemático.
.

.
CLIK AQUÍ PARA RESOLVER LA GUÍA DE ACTIVIDADES DE NÚMEROS ENTEROS
→Los números Racionales (Q): números para expresar medidas
Medir es comparar dos cantidades de una misma magnitud. Más precisamente, cada vez que expresamos numéricamente una cantidad, la estamos comparando con otra a la que llamamos unidad. Así, por ejemplo, cuando decimos que la superficie del terrero de una casa es ![]() , estamos midiendo el terreno tomando como unidad
, estamos midiendo el terreno tomando como unidad ![]() .
.
Al resultado de medir se le denomina medida; esta no suele ser un número entero. Por eso, para expresar medidas, se requiere un tipo de números que admita trozos de unidad o raciones de unidad: los números racionales.
Por ejemplo:
- tiene una temperatura corporal de 36,5°
- le ha correspondido ![]() de la herencia
de la herencia
Son medidas expresadas con números racionales. El paso siguiente es que resuelvan la situación concreta con números racionales.
"La Bombilla"- Venta de termos y mates personalizados

María y Luis sueñan con realizar un proyecto para el cuál vienen ahorrando desde hace un tiempo: planifican iniciar un emprendimiento de venta de mates y termos personalizados al que llamarán “La Bombilla”. Para esto se propusieron alquilar un pequeño inmueble en una zona comercial, luego de tanto buscar encontraron el lugar que habían soñado, pero había que hacerle algunas remodelaciones, lo que implicaría una inversión previa.
Empezaron a proyectar las remodelaciones… hay muchas mediciones y cálculos para hacer. Por eso ahora les proponemos que ayuden a María y Luis con su emprendimiento.
Deben usar el archivo que se adjunta a continuación para responder los interrogantes que tienen María y Luis. Click aquí para leer el archivo "La Bombilla"
.

.CLIK AQUÍ PARA RESPONDER EL CUESTIONARIO "La bombilla"
→PARA TENER EN CUENTA : los números decimales en la práctica
Como dijimos anteriormente, los números racionales sirven para expresar medidas y operar con ellos. En la práctica, las medidas siempre son aproximadas, por lo que los números decimales utilizados para resolver estas situaciones deben tener una cantidad de cifras decimales adecuadas, a lo que se quiere expresar y a la exactitud de las medidas que manejen.
Un número decimal puede ser aproximado por truncamiento o por redondeo. Por ejemplo:
Si no recuerdan estas técnicas de aproximación tienen la Guía de estudio para repasar el tema.
- Operaciones combinadas con decimales y fracciones
Es habitual que confundan el concepto de número racional con sus representaciones. Asimismo las distintas formas de representación de un número racional. Por eso, consideramos conveniente un tutorial sobre operaciones combinadas con números racionales en los que aparecen distintas formas de representación, las fraccionarias y las expresiones decimales finitas y periódicas. Esto les ayudará a superar tal confusión.
.

.
 .CLICK AQUÍ PARA RESOLVER LA GUÍA DE ACTIVIDADES DE NÚMEROS RACIONALES
.CLICK AQUÍ PARA RESOLVER LA GUÍA DE ACTIVIDADES DE NÚMEROS RACIONALES
→Los Números Reales (R): con las medidas también surgen los números irracionales
Además de los números decimales exactos y los periódicos existen otros decimales: los decimales de infinitas cifras no periódicas que se llaman números irracionales. Estos también resultan medidas en diversas situaciones prácticas . Nombramos algunos ejemplos con números irracionales famosos:
- El número
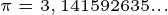 se utiliza para calcular la medida de la longitud de una circunferencia o el área de un círculo.
se utiliza para calcular la medida de la longitud de una circunferencia o el área de un círculo. - El número
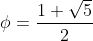 conocido como número de oro, se ha usado con mucha frecuencia en el arte.
conocido como número de oro, se ha usado con mucha frecuencia en el arte. - El número e=2,718281... aparece en fórmulas que expresan crecimientos de población animal y vegetal.
.

.
- ¿Quién fue Pitágoras?
- ¿Qué conceptos matemáticos pone en juego la demostración geométrica del famoso Teorema de Pitágoras?.
Ahora van a resolver una situación concreta que pone a los reales en acción con el Teorema de Pitágoras.
Pitágoras y los albañiles
Aunque es frecuente presuponer que el teorema recibiera su nombre porque lo inventara Pitágoras, lo más probable y cercano a la historia real, es que él consiguiera la primera demostración de que la relación entre los números 3, 4 y 5, es una propiedad de todos los triángulos rectángulos, y exclusiva sólo de ellos. Una relación, que mucho antes ya era conocida y considerada mágica, y secreta en algunos gremios. Se tiene constancia de que los antiguos, conocían no sólo ésta sino muchas más tríadas de números que guardaban entre sí, la misma relación matemática que estos tres. Pero lo que logró, en todo caso, fue dicha demostración.

El conocimiento de la relación entre los catetos y la hipotenusa de los triángulos rectángulos, por lo visto, ya era utilizado desde una más remota antigüedad. Efectivamente al menos unos miles de años antes, era conocida por babilonios y egipcios. Y no precisamente por matemáticos ilustres, sino por gente de oficios, como los oficiales de albañilería y jefes de obra. Gracias al uso de las cuerdas de 12 nudos, lograban levantar paredes en ángulos rectos perfectos, lo que los albañiles de hoy llaman "levantar".
Iniciamos la actividad utilizando una construcción realizada en Geogebra, partiendo del triángulo dado por la relación catetos 3 y 4, hipotenusa 5.
https://www.geogebra.org/m/h2umsq3c
En la sección Materiales de apoyo tienen información relativa al software GeoGebra y el link oficial (https://www.geogebra.org/)
En esta construcción del boceto del Geo pueden ver un triángulo cuya base se puede variar entre 4 y 40, la altura entre 3 y 30. Esta variación se logra moviendo los deslizadores verde y rojo respectivamente, consiguiendo triángulos rectángulos de diferentes dimensiones.
Después de mover los deslizadores en la construcción en Geogebra y analizar las relaciones que se plantean según las medidas de los lados del triángulo rectángulo, pueden responder las siguientes preguntas que proponemos en la SITUACIÓN PARA RESOLVER: Escuadra de Albañil. Relacionando números.
.

CLICK AQUÍ PARA CONTESTAR EL CUESTIONARIO Escuadra de albañil. Relacionando números
Las respuestas de este cuestionario les podrían ayudar a los albañiles en su construcción.
Traten de contactarse con un albañil y pregúntenle si conoce la relación 3,4,5 en un triángulo rectángulo, de lo contrario cuéntenle el secreto.
¿Qué sabían sobre el teorema de Pitágoras, qué saben ahora, que más les gustaría aprender?
La funcionalidad de la Matemática: Pitágoras en la construcción
Es habitual escuchar voces de estudiantes que preguntan: "¿para qué sirve esto?" o "¿por qué estudiamos esto si no lo vamos a utilizar"? . Si hay una característica que distingue a la Matemática es su funcionalidad en la vida real. Ya que estamos en una actividad en la que utilizamos el Teorema de Pitágoras, mostramos este video en el que entrevistan a un obrero de la construcción que nos cuenta cómo utiliza este teorema en su práctica. Un ejemplo, entre tantos, que da cuenta que la Matemática funciona en la realidad.
.

.
Operaciones con Números Reales
Operar con números irracionales expresados como radicales es otra actividad que deberán realizar. Les proponemos dos tutoriales sobre operaciones con radicales. Tómense el tiempo suficiente para mirar cada uno de ellos.
- División de radicales.
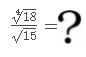
Una de las dificultades que son motivo de consultas en las clases es la división de números irracionales expresados como radicales de índices distintos. Por eso elaboramos un tutorial sobre esta operación.
.

.
Video tutorial: División de radicales de índices distintos
- Operaciones combinadas con números irracionales.
![]()
![]()
Otra de las dificultades que se plantean en las clases es: ¿cómo se resuelven las operaciones combinadas con números irracionales? Por lo cual decidimos preparar un video tutorial sobre este tema.
.

.
Video tutorial: Operaciones combinadas con números irracionales.

UN POCO DE HISTORIA
El paso de los números a las letras: las ecuaciones
El Álgebra comienza, en realidad, cuando los matemáticos empiezan a interesarse por las operaciones que se pueden hacer con cualquier número, más que por los números mismos. Ese cualquier número se representa con una letra y se da, así, el paso de la Aritmética al Álgebra.
En un principio, las operaciones generales con números cualesquiera se describían con un montón de palabras:
¿Cuánto vale la cosa que, si se triplica y se la añade diez, vale el cuadrado de la cosa?
Hacia el siglo XVII los matemáticos ya se habían dado cuenta que sería mejor tener símbolos para la cosa buscada, es decir, para la incógnita (x) y para los números que intervenían en las ecuaciones cuando no importaba qué números concretos debían ser.
En esa época, el problema anterior ya se había expresado así:
¿Cuánto es x si ![]() ?
?
Así queda planteada una expresión denominada ecuación. La palabra ecuación viene del latín aequare que significa igualar.
Fuente: De Guzmán, M., Cólera, J. y Salvador, A. (1987, p.68).
| ¿Recuerdan cómo se resuelven las ecuaciones lineales con una incógnita ? |
Como ya les planteamos al inicio del curso, siempre debemos recuperar los conocimientos que tenemos de un tema, o sea los conocimientos previos. Por eso, antes de comenzar a desarrollar algunos conceptos de ecuaciones lineales, van a realizar una actividad de autoevaluación que les permitirá valorar qué recuerdan de resolución de una ecuación lineal con una incógnita y su aplicación en la resolución de problemas. ¡Entremos en acción!

CLICK AQUÍ PARA CONTESTAR EL CUESTIONARIO DE AUTOEVALUACIÓN
.

.
¿Qué saben sobre las ecuaciones lineales con una incógnita ? ¿qué les falta aprender?
¿Qué saben sobre las ecuaciones lineales con una incógnita ? ¿qué les falta aprender?
Ahora sí iniciamos el desarrollo del tema con las explicaciones para ayudarles a aprender.
LAS ECUACIONES LINEALES CON UNA INCÓGNITA
En las actividades con números Z, Q y R, es muy probable que se les hayan presentado distintas situaciones problemáticas que pudieron resolver mediante una ecuación, como por ejemplo, el problema siguiente.
La traducción del enunciado expresado en el lenguaje coloquial al lenguaje simbólico es: ![]()
Queda así planteado el problema como una ecuación lineal con una incógnita o ecuación polinómica de primer grado con una incógnita (x).
¿Qué significa resolver una ecuación?
Una vez planteada la ecuación, hay que resolver. Para resolver conviene que sigan un orden de actuación que facilite la tarea y ayude a no cometer errores. Invitamos a que miren los videos tutoriales para afianzar sus conocimientos sobre el tema.
Resolución de ecuaciones lineales con una incógnita
Cuando se resuelve una ecuación es habitual escuchar , por ejemplo: " este número que está sumando en el primer miembro pasa restado al segundo miembro" o "este número que está multiplicando en el primer miembro pasa dividiendo al segundo miembro" .

En realidad estos pasajes se justifican con propiedades que se cumplen en las igualdades. Este tutorial muestra el procedimiento de resolución y justificación de los pasajes utilizando propiedades.
.

.
Video tutorial: Resolución de ecuaciones lineales con una incógnita
- La solución de una ecuación lineal
Generalmente se piensa que una ecuación lineal con una incógnita siempre admite una única solución, pero no es siempre así.
También está el caso en que puede admitir infinitas soluciones, es decir que se cumpla la igualdad para cualquier valor numérico de la incógnita. En este caso, la ecuación se llama Identidad. O cabe la posibilidad que la ecuación no tenga solución. En el video tutorial se resuelven estos casos.
.

Video tutorial: Resolución de ecuaciones lineales con distintos tipos de soluciones.
La resolución de problemas con ecuaciones lineales con una incógnita
La Matemática, como ciencia, surgió a partir de los problemas que enfrentó la humanidad a lo largo de la historia. Inicialmente fueron los problemas de cálculos para el comercio, para medir la Tierra y para predecir los acontecimientos astronómicos. Luego, fueron problemas cada vez más complejos y relacionados a distintos campos de estudio, como las ingenierías, la medicina, las ciencias sociales, etc.
Afirmamos que: los problemas están en el ADN del conocimiento matemático. Como lo expresan muchos matemáticos: "Hacer matemática es resolver problemas".
Con la resolución de problemas no sólo se aprenden contenidos conceptuales de Matemática, sino también se desarrollan habilidades y distintos tipos de pensamientos que te ayudarán para asumir de manera estratégica distintos desafíos que se te presentarán en la vida. Entonces, ¿qué les parece mirar este video tutorial sobre resolución de problemas utilizando ecuaciones lineales?
.

Video tutorial: Resolución de problemas con ecuaciones lineales con una incógnita
.

.
Esta Guía de actividades tiene el propósito que puedan profundizar el estudio de las ecuaciones lineales con una incógnita. No olviden que si necesitan orientación sobre el tema tienen también como material de apoyo a la Guía de estudio que les ayudará en este sentido.

CLICK AQUÍ PARA RESOLVER LA GUÍA DE ACTIVIDADES CON ECUACIONES LINEALES
| ¿Recuerdan cómo se resuelve un sistema de ecuaciones lineales ? |
Antes de desarrollar el tema es necesario valorar cuánto se recuerda del tema que vamos a aprender. Por eso les planteamos que resuelvan una actividad de autoevaluación utilizando sus conocimientos previos , y por que no , un poco de ingenio. Antes de la resolución viene la recomendación.

Para resolver cualquiera de las actividades que proponemos no deben recurrir primero a la Guía de Estudio. Precisamente lo que pretendemos es que revisen y valoren los conocimientos que tienen del tema. Luego, les invitamos a que interactúen con la Guía de Estudio para aclarar dificultades o afianzar conocimientos del tema.
.
.
Ahora sí les presentamos el problema que trata esta actividad de autoevaluación. De esta manera van a poner a prueba los conocimientos ya aprendidos de sistemas de ecuaciones lineales. ¡Entremos en acción!
.

El problema: Dos ciudades A y B distan 180 km entre sí. A las 9 de la mañana sale un coche de la ciudad A y un camión de la ciudad B. Los dos móviles van en el mismo sentido y emprenden el viaje en el mismo momento. El que sale de A circula a una velocidad constante de 90 km por hora y el que sale de B va a una velocidad constante de 60 km/hora. ¿Cuánto tiempo tardan en cruzarse el camión y el auto?.
.


CLICK AQUÍ PARA RESOLVER EL CUESTIONARIO DE SISTEMA DE ECUACIONES LINEALES

.
¿Qué saben sobre sistemas de ecuaciones lineales y qué les falta aprender ?
¿Qué saben sobre sistemas de ecuaciones lineales y qué les falta aprender ?
FICHA DE ESTUDIO
Para comprender sistemas de dos ecuaciones lineales con dos incógnitas necesitan tener claridad sobre qué es una ecuación lineal con dos incógnitas, sus soluciones y la representación gráfica de las soluciones. La ficha de estudio les ayudará a recordar conceptos de este tipo de ecuaciones. Lean de manera reflexiva esta ficha.
.

.
Escriban un argumento convincente explicando por qué la ecuación \(x=4+\frac{7}{y}\) no es lineal con dos incógnitas
UN POCO DE HISTORIA
Dos milenios antes de Cristo, en la Mesopotamia asiática, se había avanzado notablemente en el camino de la resolución de los sistemas de ecuaciones lineales. Los sistemas fueron resueltos por los babilonios, los cuales llamaban a las incógnitas con palabras tales como longitud, anchura, área, o volumen , sin que tuvieran relación con problemas de medida.
Un ejemplo tomado de una tablilla babilónica plantea la resolución de un sistema de ecuaciones en los siguientes términos:
¼anchura + longitud = 7 manos
longitud + anchura = 10 manos
Para resolverlo comienzan asignando el valor 5 a una mano y observaban que la solución podía ser: anchura = 20, longitud = 30
Los griegos también resolvían algunos sistemas de ecuaciones, pero utilizando métodos geométricos. Thymaridas (400 a. de C.) había encontrado una fórmula para resolver un determinado sistema de n ecuaciones con n incógnitas.
Diophante resuelve también problemas en los que aparecían sistemas de ecuaciones, pero transformándolos en una ecuación lineal.
Diophante sólo aceptaba las soluciones positivas, pues lo que buscaba era resolver problemas y no ecuaciones. Utilizó ya un álgebra sincopada como hemos señalado anteriormente. Sin embargo, unas de las dificultades que encontramos en la resolución de ecuaciones por Diophante es que carece de un método general y utiliza en cada problema métodos a veces excesivamente ingeniosos.
Los sistemas de ecuaciones aparecen también en los documentos indios. No obstante, no llegan a obtener métodos generales de resolución, sino que resuelven tipos especiales de ecuaciones.
Fuente: https://thales.cica.es/rd/Recursos/rd98/Matematicas/14/historia.html
| ¿Qué es un sistema de ecuaciones? ¿qué significa resolver un sistema? |
Los sistemas de ecuaciones son muy interesantes por las diversas situaciones prácticas que permiten resolver. Para tener claridad sobre cuáles son las situaciones en las que debemos plantear un sistema es necesario es necesario saber qué es un sistema de ecuaciones lineales y qué significa resolverlo. El video tutorial trata sobre ello.
.

Video tutorial: Concepto de sistemas de ecuaciones lineales
Resolución de sistemas de ecuaciones lineales de 2x2
Como vieron en el video tutorial resolver un sistema de ecuaciones lineales con dos incógnitas significa hallar, si es que existen, las soluciones comunes a las dos ecuaciones del sistema. Hay diferentes métodos para resolver sistemas, uds podrán utilizar el que prefieran, aunque en algunos casos verán que es más cómodo alguno en particular.
Les presentamos tres videos tutoriales sobre tres métodos de resolución de sistemas: gráfico, igualación y sustitución. Vale aclararles que existen otros métodos de resolución.
- Método gráfico
.

Video tutorial: Método gráfico de resolución de sistemas de 2x2
El método gráfico es un procedimiento que permite hacer la interpretación geométrica de la solución del sistema. No se olviden que de acuerdo a las posiciones relativas de las rectas el sistema de ecuaciones de 2x2 tendrá o no solución.
https://www.geogebra.org/m/rg77dnv3
Ingresen al boceto del Geo y consideren los deslizadores que son los valores que toman los coeficientes y términos independientes de un sistema de 2x2 cuya expresión genérica es:
Analicen las posiciones relativas de las rectas a partir de mover los deslizadores y observen qué relaciones existen entre las ecuaciones de las rectas y las posibles soluciones del sistema. Respondan:
- ¿Qué relación se debe plantear entre los coeficientes y términos independientes de las dos ecuaciones del sistema para que éste sea compatible determinado/compatible indeterminado o incompatible?
- Método de igualación

Video tutorial: Método de igualación de resolución de sistemas de 2x2
El método de igualación, a diferencia del método anterior, es un método algebraico. Con este método podemos calcular, si es que existen, los valores exactos de cada par (x , y) que verifica las ecuaciones del sistema.
- Método de sustitución

Video tutorial: Método de sustitución de resolución de sistemas de 2x2
El método de sustitución es otro método algebraico. Con este método también podemos calcular, si es que existen, los valores exactos de cada par (x , y) que verifica las ecuaciones del sistema.
FICHA DE ESTUDIO
Es importante que conozcan varios métodos de resolución de sistemas porque les permitirá elegir, en cada caso, el que les parezca más sencillo. También que puedan relacionar las interpretaciones geométricas y algebraicas de las soluciones que dan lugar a la clasificación de los sistemas de ecuaciones . La ficha de estudio que viene a continuación les ayudará a recordar estas relaciones. Lean de forma reflexiva la ficha.

.
Con esta guía de actividades van a poner en juego los conceptos de sistemas de ecuaciones desarrollados en este bloque. No olviden que si necesitan orientación sobre el tema tienen también la Guía de estudio que les ayudará en este sentido.
.

CLICK AQUÍ PARA RESOLVER LA GUÍA DE ACTIVIDADES DE SISTEMAS DE ECUACIONES LINEALES
¿Qué dificultades matemáticas han tenido? ¿Qué estrategias utilizaron para superar las dificultades?

CUESTIONARIO DE EVALUACIÓN FINAL DEL BLOQUE 1
Y ha llegado el momento de la autoevaluación final del Bloque I. Esta actividad forma parte del aprendizaje porque también deben aprender a valorar, criticar y a reflexionar sobre el proceso de aprendizaje individual realizado.


CLICK AQUÍ PARA RESPONDER EL CUESTIONARIO DE EVALUACIÓN FINAL DEL BLOQUE I
.

- ¿Qué sabían sobre los temas del bloque 1? ¿Qué saben ahora? ¿Qué más les gustaría aprender relacionado a estos temas?
- ¿Qué han aprendido de ustedes mismos en relación con la Matemática?
- ¿Qué sabían sobre los temas del bloque 1? ¿Qué saben ahora? ¿Qué más les gustaría aprender relacionado a estos temas?
- ¿Qué han aprendido de ustedes mismos en relación con la Matemática?
Para finalizar este bloque compartimos el excelente vídeo de Cristóbal Vila que nos muestra la presencia de los números y la geometría en la naturaleza con una secuencia de imágenes excepcional.
.

¿Quién se animaría a decir que la matemática no tiene belleza? 😍





