Logaritmación
| Sitio: | Educación a Distancia - UNaM |
| Curse: | Matemática |
| Libro: | Logaritmación |
| Impreso por: | Cuenta visitante |
| Fecha: | lunes, 17 de noviembre de 2025, 17:02 |
Descripción
VES 2022
LOGARITMACIÓN
¿RECUERDAN CUÁLES SON LAS OPERACIONES INVERSAS DE LA POTENCIACIÓN?
Así como la operación inversa de la adición es la sustracción y la operación inversa de la multiplicación es la división, las dos operaciones inversas de la potenciación son: la radicación y la logaritmación. De esta manera definimos entonces la logaritmación como una de las operaciones inversas de la potenciación.
Antes de repasar la operación logaritmación les proponemos, como en los otros bloques, que resuelvan una actividad de autoevaluación para valorar sus conocimientos de este tema.

CLICK AQUI PARA CONTESTAR EL CUESTIONARIO DE AUTOEVALUACIÓN DE LOGARITMACIÓN

¿Qué saben de la operación Logaritmación? ¿qué les falta aprender ?
¿Qué saben de la operación Logaritmación? ¿qué les falta aprender ?
Hagamos memoria
La logaritmación surge de los problemas que se plantean cuando se desea hallar el exponente de una potencia. Para resolver este tipo de problemas es necesario saber cómo se define esta operación. Este tutorial les ayudará a comprender la definición de logaritmación.

Video tutorial: Definición de logaritmación
¿Por qué la potenciación tiene dos operaciones inversas?
(Para poder responder esta pregunta les sugerimos que resuelvan estos ejercicios)
Propiedades de la logaritmación
De igual modo que en las otras operaciones (suma, resta, multiplicación, división, potenciación y radicación), en la logaritmación se cumplen propiedades. En el tutorial se explican algunas de ellas.

Video tutorial: Propiedades de los logaritmos
La siguiente FICHA DE ESTUDIO es un recurso para recordar las propiedades desarrolladas en el tutorial. Recordémoslas:
Algunas calculadoras están preparadas para obtener directamente los logaritmos decimales (con base 10) o los logaritmos nepperiano (con base e). En esas calculadoras encuentran dos teclas.
En el tutorial también está la explicación de cómo calcular logaritmos en otras bases.
¡TENGAN EN CUENTA!
Un ejemplo de aplicación
Una gran variedad de problemas se resuelven utilizando logaritmos. El problema que les presentamos a continuación es un ejemplo de aplicación de esta operación.
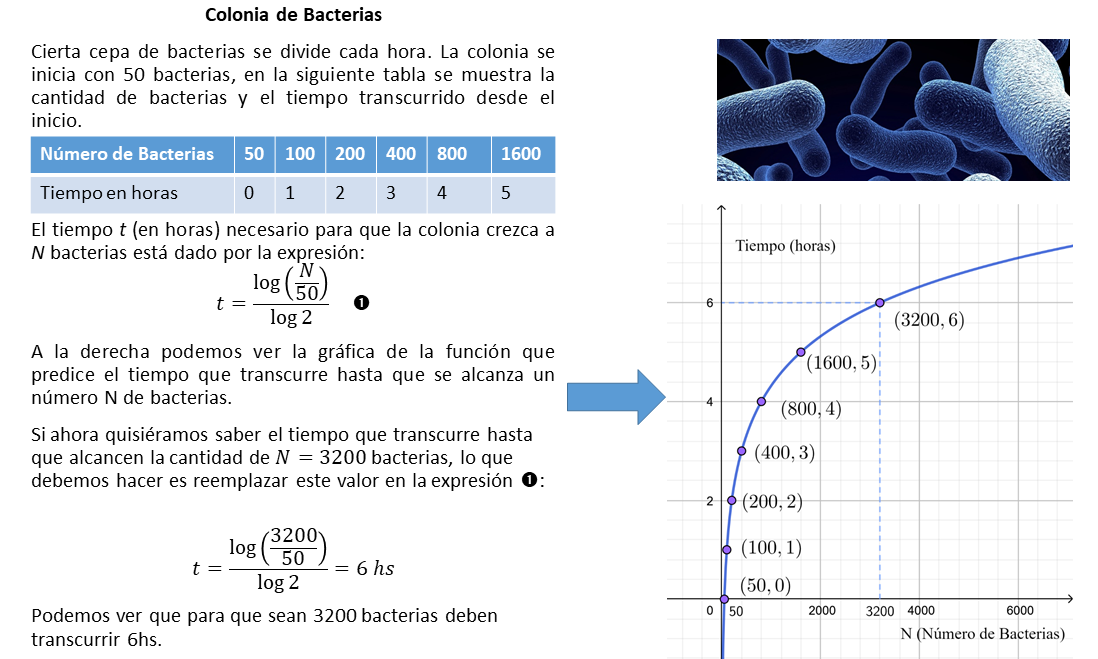
En este ejemplo de aplicación pueden observar la gráfica de una función. El concepto de función y su utilidad para describir, analizar e interpretar situaciones de la matemática y otras ciencias, hemos desarrollado en el Bloque III. En este caso particular, la función describe la relación entre la cantidad de bacterias y el tiempo. La gráfica de esta función nos permite verificar el valor hallado mediante cálculos utilizando su fórmula que está afectada por la operación logaritmación.
Si bien en este curso no nos dedicaremos a estudiar la función logarítmica, para quienes estén dispuestos a profundizar un poco más les proponemos esta actividad de investigación que les permitirá analizar cómo se comportan las funciones logarítmicas.
¿Cuál es tu conclusión?
- Considerar la función logarítmica de la forma:
e interpretar la variación de la función en relación con la variación de la base o del argumento ( Experimenten con el Geo y utilicen los deslizadores).
- ¿Cómo se comporta la gráfica de la función cuando b>0?
- ¿Cómo se comporta la gráfica de la función cuando 0<b<1?
- ¿En qué valor corta la gráfica de la función
al eje de abscisas?¿Por qué?
- ¿Cómo se comporta la función si hacemos variar el argumento, considerando los casos planteados en los puntos 2. y 3. ?
https://www.geogebra.org/m/hg5wjg8x
Otra de las situaciones matemáticas en la que aplica la logaritmación y sus propiedades es en la resolución de ecuaciones exponenciales y logarítmicas. Aquí trabajaremos este tipo de ecuaciones, pero solamente aquéllas que son muy sencillas. Las más complejas dejamos para otro curso.
ECUACIONES EXPONENCIALES Y LOGARÍTMICAS
Una ecuación en la que la incógnita aparece en el exponente, se llama ecuación exponencial. Por ejemplo: . Para resolver estas ecuaciones se utilizan los logaritmos. De ahí es que las propiedades y el cálculo de logaritmos van a servir de gran ayuda para la resolución de ecuaciones exponenciales.
Hay otro tipo de ecuaciones muy relacionadas con las exponenciales: las logarítmicas. En ellas la incógnita aparece en una expresión afectada por un logaritmo. Por ejemplo:
Les invitamos a que miren este tutorial en el que se explica muy bien cómo se resuelven las ecuaciones exponenciales y logarítmicas.

Video tutorial: Resolución de ecuaciones logarítmicas y exponenciales
La FICHA DE ESTUDIO les presenta dos ejemplos de resolución de este tipo ecuaciones que les ayudará a recordar algunos aspectos que deben tener en cuenta para trabajar en este tema.
¿Qué les parece si se ponen a practicar los conocimientos desarrollados de logaritmación? Con esta intención les proponemos que resuelvan los ejercicios y problemas de esta guía de actividades. ¡ADELANTE!.

CLICK AQUÍ PARA RESOLVER LA GUÍA DE ACTIVIDADES DE LOGARITMACIÓN
¿Qué dificultades matemáticas han tenido? ¿Qué estrategias utilizaron para superar las dificultades?

CUESTIONARIO DE EVALUACIÓN FINAL DEL BLOQUE 4
Ahora llegó el momento de la autoevaluación final del Bloque 4. No olviden que esta actividad forma parte de este proceso de aprendizaje que están transitando. Tengan en cuenta que es tan importante aprender con sentido los conceptos matemáticos como aprender a valorar, criticar y a reflexionar sobre el proceso de aprendizaje individual realizado.


CLICK AQUÍ PARA CONTESTAR EL CUESTIONARIO

¿Qué sabían sobre los conceptos del bloque IV, qué saben ahora, que más les gustaría aprender relacionado a logaritmación?
¿Qué sabían sobre los conceptos del bloque IV, qué saben ahora, que más les gustaría aprender relacionado a logaritmación?

